Rumus - Rumus Minimal
Hukum Newton I Σ F = 0
→ benda diam atau
→ benda bergerak dengan kecepatan konstan / tetap atau
→ percepatan gerak benda nol atau
→ benda bergerak lurus beraturan (GLB)
Hukum Newton II Σ F = ma
→ benda bergerak dengan percepatan tetap
→ benda bergerak lurus berubah beraturan (GLBB)
→ kecepatan gerak benda berubah
Gaya Gesek Gaya Gesek Statis → f
s = μ
s N
Gaya Gesek Kinetis → f
k = μ
k N
dengan N = gaya normal, μ
s = koefisien gesek statis, μ
k = koefisien gesek kinetis
Gaya Berat W = mg
Contoh Soal dan Pembahasan
Soal No. 1 Perhatikan gambar berikut!

Benda
bermassa m = 10 kg berada di atas lantai kasar ditarik oleh gaya F = 12
N ke arah kanan. Jika koefisien gesekan statis antara benda dan lantai
adalah 0,2 dengan koefisien gesekan kinetis 0,1 tentukan besarnya :
a) Gaya normal
b) Gaya gesek antara benda dan lantai
c) Percepatan gerak benda
PembahasanGaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ F
y = 0
N − W = 0
N − mg = 0
N − (10)(10) = 0
N = 100 N
b) Gaya gesek antara benda dan lantai
Cek terlebih dahulu gaya gesek statis maksimum yang bisa terjadi antara benda dan lantai:
f
smaks = μ
s N
f
smaks = (0,2)(100) = 20 N
Ternyata gaya gesek statis maksimum masih lebih besar dari gaya yang
menarik benda (F) sehingga benda masih berada dalam keadaan diam. Sesuai
dengan hukum Newton untuk benda diam :
Σ F
x = 0
F − f
ges = 0
12 − f
ges = 0
f
ges = 12 N
c) Percepatan gerak benda
Benda dalam keadaan diam, percepatan benda NOL
Soal No. 2 Perhatikan gambar berikut, benda mula-mula dalam kondisi rehat!

Benda
bermassa m = 10 kg berada di atas lantai kasar ditarik oleh gaya F = 25
N ke arah kanan. Jika koefisien gesekan statis antara benda dan lantai
adalah 0,2 dengan koefisien gesekan kinetis 0,1 tentukan besarnya :
a) Gaya normal
b) Gaya gesek antara benda dan lantai
c) Percepatan gerak benda
d) Jarak yang ditempuh benda setelah 2 sekon
Pembahasan Gaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ F
y = 0
N − W = 0
N − mg = 0
N − (10)(10) = 0
N = 100 N
b) Gaya gesek antara benda dan lantai
Cek terlebih dahulu gaya gesek statis maksimum yang bisa terjadi antara benda dan lantai:
f
smaks = μ
s N
f
smaks = (0,2)(100) = 20 N
Ternyata gaya yang gesek statis maksimum (20 N) lebih kecil dari gaya
yang menarik benda (25 N), Sehingga benda bergerak. Untuk benda yang
bergerak gaya geseknya adalah gaya gesek dengan koefisien gesek kinetis :
f
ges = f
k = μ
k N
f
ges = (0,1)(100) = 10 N
c) Percepatan gerak benda
Hukum Newton II :
Σ F
x = ma
F − f
ges = ma
25 − 10 = 10a
a =
15/
10 = 1,5 m/s
2 d) Jarak yang ditempuh benda setelah 2 sekon
S = V
o t +
1/
2 at
2 S = 0 +
1/
2(1,5)(2
2)
S = 3 meter
Soal No. 3 Perhatikan gambar berikut, benda 5 kg mula-mula dalam kondisi tidak bergerak!

Jika sudut yang terbentuk antara gaya F = 25 N dengan garis mendatar adalah 37
o, koefisien gesek kinetis permukaan lantai adalah 0,1 dan percepatan gravitasi bumi 10 m/s
2 tentukan nilai:
a) Gaya normal
b) Gaya gesek
c) Percepatan gerak benda
(sin 37
o = 0,6 dan cos 37
o = 0,8)
Pembahasan Gaya-gaya pada benda diperlihatkan gambar berikut:

a) Gaya normal
Σ F
y = 0
N + F sin θ − W = 0
N = W − F sin θ = (5)(10) − (25)(0,6) = 35 N
b) Gaya gesek
Jika dalam soal hanya diketahui koefisien gesek kinetis, maka dipastikan benda bisa bergerak, sehingga f
ges = f
k :
f
ges = μ
k N
f
ges = (0,1)(35) = 3,5 N
c) Percepatan gerak benda
Σ F
x = ma
F cos θ − f
ges = ma
(25)(0,8) − 3,5 = 5a
5a = 16,5
a = 3,3 m/s
2 Soal No. 4 Perhatikan gambar berikut, balok 100 kg diluncurkan dari sebuah bukit!

Anggap lereng bukit rata dan memiliki koefisien gesek 0,125. Percepatan gravitasi bumi 10 m/s
2 dan sin 53
o = 0,8, cos 53
o = 0,6. Tentukan nilai dari :
a) Gaya normal pada balok
b) Gaya gesek antara lereng dan balok
c) Percepatan gerak balok
Pembahasan Gaya-gaya pada balok diperlihatkan gambar berikut:
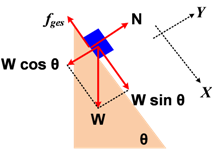
a) Gaya normal pada balok
Σ F
y = 0
N − W cos θ = 0
N − mg cos 53
o = 0
N − (100)(10)(0,6) = 0
N = 600 Newton
b) Gaya gesek antara lereng dan balok
f
ges = μ
k N
f
ges = (0,125)(600) = 75 newton
c) Percepatan gerak balok
Σ F
x = ma
W sin θ − f
ges = ma
mg sin 53
o − f
ges = ma
(100)(10)(0,8) − 75 = 100a
a =
725/
100 = 7,25 m/s
2 Soal No. 5
Balok A massa 40 kg dan balok B massa 20 kg berada di atas permukaan
licin didorong oleh gaya F sebesar 120 N seperti diperlihatkan gambar
berikut!

Tentukan :
a) Percepatan gerak kedua balok
b) Gaya kontak yang terjadi antara balok A dan B
Pembahasan a) Percepatan gerak kedua balok
Tinjau sistem :
Σ F = ma
120 = (40 + 20) a
a =
120/
60 m/s
2 b) Gaya kontak yang terjadi antara balok A dan B
Cara pertama, Tinjau benda A :

Σ F = ma
F − F
kontak = m
A a
120 − F
kontak = 40(2)
F
kontak = 120 − 80 = 40 Newton
Cara kedua, Tinjau benda B :

Σ F = ma
F
kontak = m
B a
F
kontak = 20(2) = 40 Newton
Soal No. 6
Balok A dan B terletak pada permukaan bidang miring licin didorong oleh
gaya F sebesar 480 N seperti terlihat pada gambar berikut!
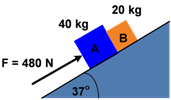
Tentukan :
a) Percepatan gerak kedua balok
b) Gaya kontak antara balok A dan B
Pembahasan a) Percepatan gerak kedua balok
Tinjau Sistem :
Gaya-gaya pada kedua benda (disatukan A dan B) terlihat pada gambar berikut:
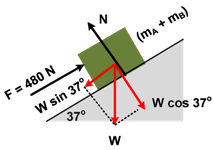
Σ F = ma
F − W sin 37
o = ma
480 − (40 + 20)(10)(0,6) = (40 + 20) a
a =
120/
60 = 2 m/s
2 b) Gaya kontak antara balok A dan B
Cara pertama, tinjau balok A
Gaya-gaya pada balok A terlihat pada gambar berikut :

Σ F = ma
F − W
A sin 37
o − F
kontak = m
A a
480 − (40)(10) (0,6) − F
kontak = (40)(2)
480 − 240 − 80 = F
kontak F
kontak = 160 Newton
Cara kedua, tinjau benda B
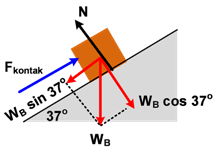
Σ F = ma
F
kontak − W
B sin 37
o = m
B a
F
kontak − (20)(10)(0,6) =(20)(2)
F
kontak = 40 + 120 = 160 Newton
Soal No. 7 
Balok A beratnya 100 N diikat dengan tali mendatar di C (lihat gambar).
Balok B beratnya 500 N. Koefisien gesekan antara A dan B = 0,2 dan
koefisien gesekan antara B dan lantai = 0,5. Besarnya gaya F minimal
untuk menggeser balok B adalah....newton
A. 950
B. 750
C. 600
D. 320
E. 100
(Sumber Soal : UMPTN 1993) Pembahasan fAB → gaya gesek antara balok A dan B
fBL → gaya gesek antara balok B dan lantai
fAB = μ
AB N
fAB = (0,2)(100) = 20 N
fBL = μ
BL N
fBL = (0,5)(100 + 500) = 300 N
Tinjau benda B

Σ F
x = 0
F −
fAB −
fBL = 0
F − 20 − 300 = 0
F = 320 Newton
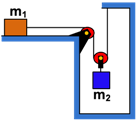
Soal No. 8 Benda pertama dengan massa m
1 = 6 kg dan benda kedua dengan massa m
2 = 4 kg dihubungkan dengan katrol licin terlihat pada gambar berikut !

Jika lantai licin dan m
2 ditarik gaya ke kanan F = 42 Newton, tentukan :
a) Percepatan benda pertama
b) Percepatan benda kedua
c) Tegangan tali T
Pembahasan a) Percepatan benda pertama
Hubungan antara percepatan benda pertama (a
1) dan percepatan benda kedua (a
2) adalah:
a
1 = 2a
2 atau
a
2 =
1/
2a
1 Tinjau m
2 
F − 2T = m
2a
2 42 − 2T = 4a
2 42 − 2T = 4(
1/
2)a
1 42 − 2T = 2a
1 (Pers. 1) Tinjau m
1 
T = m
1a
1 T = 6 a
1 (Pers. 2) Gabung
Pers. 1 dan
Pers. 2 42 − 2T = 2a
1 42 − 2(6a
1) = 2a
1 42 = 14 a
1 a
1 =
42/
14 = 3 m/s
2 b) Percepatan benda kedua
a
2 =
1/
2a
1 a
2 =
1/
2(3) = 1,5 m/s
2 c) Tegangan tali T
T = 6a
1 = 6(3) = 18 Newton
Soal No. 9 Massa A = 4 kg, massa B = 6 kg dihubungkan dengan tali dan ditarik gaya F = 40 N ke kanan dengan sudut 37
o terhadap arah horizontal!

Jika koefisien gesekan kinetis kedua massa dengan lantai adalah 0,1 tentukan:
a) Percepatan gerak kedua massa
b) Tegangan tali penghubung antara kedua massa
Pembahasan Tinjauan massa B :
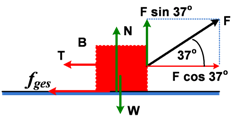
Nilai gaya normal N :
Σ F
y = 0
N + F sin 37
o = W
N + (40)(0,6) = (6)(10)
N = 60 − 24 = 36 N
Besar gaya gesek :
fgesB = μ
k N
fgesB = (0,1)(36) = 3,6 N
Hukum Newton II:
Σ F
x = ma
F cos 37
o −
fgesB − T = ma
(40)(0,8) − 3,6 − T = 6 a
28,4 − T = 6 a → (persamaan 1)
Tinjauan gaya-gaya pada massa A

Σ F
x = ma
T −
fgesA = ma
T − μ
k N = ma
T − μ
k mg = ma
T − (0,1)(4)(10) = 4 a
T = 4a + 4 → Persamaan 2
Gabung 1 dan 2
28,4 − T = 6 a
28,4 − ( 4a + 4) = 6 a
24,4 = 10a
a = 2,44 m/s
2 b) Tegangan tali penghubung antara kedua massa
T = 4a + 4
T = 4(2,44) + 4
T = 13,76 Newton
Soal No. 10 Diberikan gambar sebagai berikut!
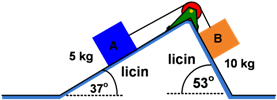
Jika massa katrol diabaikan, tentukan:
a) Percepatan gerak kedua benda
b) Tegangan tali penghubung kedua benda
Pembahasan Tinjau A

Σ F
x = ma
T − W
A sin 37
o = m
A a
T − (5)(10)(0,6) = 5 a
T − 30 = 5a → (Persamaan 1)
Tinjau B
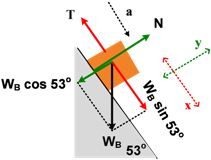
Σ F
x = ma
W
B sin 53
o − T = m
B a
(10)(0,8) − T = 10 a (10)(10)(0,8) − T = 10 a
80 − T = 10a
T = 80 − 10 a → (Persamaan 2)
Gabung 1 dan 2
T − 30 = 5a
(80 − 10 a) − 30 = 5 a
15 a = 50
a =
50/
15 =
10/
3 m/s
2 b) Tegangan tali penghubung kedua benda
T − 30 = 5a
T − 30 = 5(
10/
3)
T = 46,67 Newton
Soal No. 11 Diberikan gambar sebagai berikut:

Massa balok A = 6 kg, massa balok B = 4 kg. Koefisien gesekan kinetis
antara balok A dengan B adalah 0,1 dan koefisien gesekan antara balok A
dengan lantai adalah 0,2. Tentukan besar gaya F agar balok A bergerak
lurus beraturan ke arah kanan, abaikan massa katrol!
Pembahasan Tinjau B

Benda bergerak lurus beraturan → a =0
Σ F
x = 0
T −
fBA =0
T =
fBA = μ
BA N = μ
BA mg= (0,1)(4)(10) = 4 N
Tinjau A

Σ F
x = 0
F − T −
fAB −
fAL = 0
dengan
fAL =
μAL N = (0,2)(10)(10) = 20 N
(Gaya normal pada A adalah jumlah berat A ditambah berat B, karena ditumpuk)
Sehingga :
F − 4 − 4 − 20 = 0
F = 28 Newton
Soal No. 12 Sebuah elevator bermassa 400 kg bergerak vertikal ke atas dari keadaan diam dengan percepatan tetap 2 m/s
2. Jika percepatan gravitasi 9,8 m/s
2 , maka tegangan tali penarik elevator adalah....
A. 400 newton
B. 800 newton
C. 3120 newton
D. 3920 newton
E. 4720 newton
(Sumber Soal : Proyek Perintis I 1981) Pembahasan 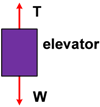
Σ F
y = ma
T − W = ma
T − (400)(9,8) =(400)(2)
T = 800 + 3920 = 4720 Newton
Soal No. 13 Dari soal nomor 12, tentukan tegangan tali penarik elevator jika gerakan elevator adalah ke bawah!
Pembahasan Elevator bergerak ke bawah :
Σ F
y = ma
W − T = ma
(400)(9,8) − T = (400)(2)
T = 3920 − 800 = 3120 Newton
Soal No. 14 Perhatikan susunan dua buah benda berikut ini:
Koefisien gesekan kinetis antara massa pertama dengan lantai adalah 0,1
, massa benda pertama = 4 kg dan massa benda kedua 6 kg. Tentukan :
a) Percepatan gerak benda pertama
b) Percepatan gerak benda kedua
Pembahasan a) Percepatan gerak benda pertama
Hubungan percepatan benda pertama dan benda kedua adalah :
a
1 =2a
2 atau
a
2 =
1/
2a
1 Tinjau benda pertama

Σ F
x = m
1a
1 T −
f = 4 a
1 T −
μk N = 4a
1 T − (0,1)(4)(10) = 4 a
1 T = 4a
1 + 4 → Persamaan 1
Tinjau benda kedua

Σ F
y = m
2a
2 W − 2T = (6)(
1/
2 a
1)
60 − 2T = 3a
1 → Persamaan 2
Gabung Persamaan 2 dan Persamaan 1
60 − 2T = 3 a
1 60 − 2(4a
1 + 4) = 3a
1 60 − 8a
1 − 8 = 3a
1 52 = 11a
1 a
1 =
52/
11 m/s
2 b) Percepatan gerak benda kedua
a
2 =
1/
2 a
1 a
2 =
1/
2 (
52/
11 ) =
26/
11 m/s
2 Soal No. 15 Balok m bermassa 10 kg menempel pada dinding kasar dengan koefisien gesekan kinetis 0,1. Balok mendapat gaya horizontal F
2 = 50 N dan gaya vertikal F
1 .
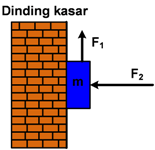
Tentukan besar gaya vertikal F
1 agar balok bergerak vertikal ke atas dengan percepatan 2 m/s
2 !
Pembahasan Tinjauan gaya yang bekerja pada m :
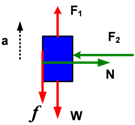
Σ F
x = 0
N − F
2 = 0
N − 50 = 0
N = 50 Newton
Σ F
y = ma
F
1 − W −
f = ma
F
1 − mg − μ
k N = ma
F
1 − (10)(10) − (0,1)(50) = 10(2)
F
1 = 20 + 100 + 5 = 125 Newton
Soal Latihan Soal Latihan No.1 Benda bermassa 4 kg diberi kecepatan awal 10 m/s dari ujung bawah bidang miring seperti gambar.

Benda mengalami gaya gesek dari bidang sebesar 16 N dan sinα =0,85. Benda berhenti setelah menempuh jarak
(A) 3 m
(B) 4 m
(C) 5 m
(D) 6 m
(E) 8 m
(Sumber Soal : UM UGM 2009) Soal Latihan No. 2
Lima buah benda (sebutlah balok), masing-masing bermassa 2 kg, 3 kg, 4
kg, 5 kg dan 6 kg, dihubungkan dengan tali-tali tanpa massa (halus),
lalu ditarik mendatar di atas lantai dengan gaya sebesar 40 N seperti
gambar di bawah.

Koefisien gesek antara masing-masing benda dan lantai 0,1, percepatan gravitasi 10 m/s
2. Tentukan besar tegangan tali penghubung benda :
a) 2 kg dan 3 kg
b) 4 kg dan 5 kg
Read more:
http://fisikastudycenter.com/fisika-xi-sma/11-dinamika-2-gaya-gesek#ixzz2mhXxQZMC

















































![clip_image002[39] clip_image002[39]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjDdiTBbQfQzs1S3ZJftmkcs7iaBnfSpS06JTxnsiccPKvEBKuapK1GkMoQxYERshrgVzwdFxxcVAI_qp19fne_9EW7KMgRuJUuLxF7J6MTj7r4a5w94piHQCBQzjYQtpDzxFrweM2jYAw/?imgmax=800)